19.1.ベアトリクス

筆者はファイナルファンタジー（FF）のシリーズが大好きです．

特にFF4，FF6，FF9あたりがいかにもファイナルファンタジーな世界観で気に入っています．

ここに一人の女性がいます．その名はベアトリクス．

FF9に登場する将軍です．

プルメシアにおいて初めて彼女と一戦交えたときは瞬殺でした．

「おのれの浅はかさを悔いるのです」

とまで言われて．次にクレイラでは，

「ざれ事もここまでです！」

ちょっと！「ざれ事」ですってよ！一生懸命やってるのに！！

あぁ…ベアトリクスにしろ，FF6のセリスにしろ，FF13のライトニングにしろ，筆者が発見した「FF女性キャラ・ア段ウ段の法則」に従う名前の末尾がウ段で終わるキャラ・・大好き．．

閑話休題…

その後いろいろあって，彼女は主に反旗を翻して仲間になります．

そしてとても心強く頼もしい同志として旅を続けていくのでした．

筆者にとって数学はベアトリクスでした．

最初は怖かった．

でも今は仲間として，とても助けになる心強いヤツです．

すると，もっとベアトリクス，もとい，数学を知りたい！と思うようになって，学生時代には1回だけ授業に出て「こらアカン！」と切り捨てたいろんな数学を今，勉強しているところです．

そしてそれは宇宙工学の研究の新しい切り口を見い出し，これを進めていく強力な手段となっています．

数学は，見た目は確かにイカツイ．

しかし味方になると人類，宇宙の困窮を解決し，シアワセな未来を創造することを強力に手伝ってくれるものなのです．

19.2.たろうくんとおかし

そもそも「数学」ってなんだろうか．

こんなの（二次方程式の解の公式）

$$ ax^2 + bx + c = 0, \quad x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

とか，こんなの（パーセバルの等式）

$$ \frac{1}{L} \int_{-L}^L {\left[f(x)\right]}^2 \mbox{d}x = \frac{a_0^2}{2} + \sum_{n=1}^{\infty} \left(a_n^2+b_n^2\right) $$

とか，こんなの（ピタゴラスの定理）

とかいう「おえっ」となりそうな，とにかく訳の分からない数式やら図形やらであると思われることが多いのではないでしょうか．

でもお待ちください．原点回帰しまして，

もんだい

　　たろうくんがおかしを1つもっています．

　　するとはなこさんがやってきて，たろうくんにおかしを2つあげました．

　　たろうくんがもっているおかしはぜんぶでいくつでしょうか．

というのはどうでしょうか．

こたえ

　　$1 + 2 = 3$　　だから3こ

ハイ，せいかい！

なめとんか！これは「数学」やのうて「算数」やないかいっ！

実は小学校1年生で習うこのような算数，簡単なようでいて，この宇宙のシクミとか，かなり難しい「数学」としての取り決めの上に成り立っています．

そもそも，たろうくんの持っているお菓子が「●」であって，それにはなこさんからの「●●」を合わせると「●●●」になる，という，いまそこに幾つかのお菓子があってその数量が変化するというこの宇宙の中での「事象」が，人間が考案した数量とその変化を表す「数の概念」とその「演算」による結果と一致しているという事実は，実は極めてスゴイことなのです．

この宇宙の事象を表現するのに必ずしも「数学」が唯一手段ではありません．

音楽でも良いし，文学でも良いです．

しかし好き嫌いや信じる信じないなどに拘らず，事象を客観的，普遍的に定性的かつ定量的に表現するには，数学は今のところ極めて有効かつ強力な手段です．

なぜなら数学とは，ある一定の厳格なルールに従って推論を行うことで，幾つかの知っていることから未だ知られていないことを，信念信条気分性格に依存せずに導くことができるからです．

なぜそんなにうまくいくのか？

まず，実際に「●」と「●●」を合わせると「●●●」になるという事象がこの宇宙には存在しているということです．

例えば，「●」と「●●」を合わせると「●●●」になりますが，「●」と「●●●」を合わせても「●●●」になる…ということはありませんよね．

当たり前過ぎるほどに当たり前のように感じるのは，私たちがこの宇宙の事象にすっかり慣れ親しんでいる証です．

次に，「数の概念」と「演算」とがあって，それ自体とその結果とが実に破綻することなく成立しているということです．

例えば，「$ 1+2=3 $」になりますが，「$ 1+3=3 $」になる…ということは間違っていますよね．

私たちは小学1年生のときから，その前提となる厳密な公理を教えられることなく，このような「数の概念」と「演算」とを次々と教えられているのです．

「モノの個数」を表すような数の概念は「自然数」と呼ばれているものです．

自然数は記号 $\mathbb{N}$ を使って表し，「ペアノの公理」として以下のような自明の性質（公理）を持つとされています．

なお，$\forall$ や $\nexists$ は数理論理学における量化子と呼ばれ，それぞれ「全ての」と「存在しない」ということを意味しています．また，$a \in B$ は「$a$ は $B$ という集合に含まれる要素である」，$A \subset B$ は「$A$ という集合は $B$ という集合の中の一部である」ということを表しています．「s.t. (such that)」は文字通り「～のような」，「$\to$」は「ならば」，「$A \mid B$」は「$B$ であるところの $A$」などと読みます．

① $ 0 := \phi \in \mathbb{N} $

　　→「何も無い（記号 $\phi$）」ことを表す自然数「0」が存在する．

② $ \forall a \in \mathbb{N} \quad \mbox{suc}(a) := a + 1 $

　　→自然数には必ず「その次の数（successor）」が存在する．

③ $ \nexists a \in \mathbb{N} \quad \mbox{s.t.} \quad \mbox{suc}(a) = 0 $

　　→「0」はいかなる自然数の「その次の数」でもない．

④ $ a \ne b \mid a,\ b \in \mathbb{N} \quad \to \quad \mbox{suc}(a) \ne \mbox{suc}(b) $

　　→異なる自然数の「その次の数」は異なる自然数である．

⑤ $ \forall S \subset \mathbb{N} \mid (0 \in S, (a \in S \to \mbox{suc}(a) \in S)) \quad \to \quad S=\mathbb{N} $

　　→自然数は同じ性質を持つ唯一の集合である．

日本語でおｋ

百歩譲って言いたいことは分かった．でも当たり前のことだろ？

ですよね．．

でもそれが「数学」です．

「数学」という言葉或いは記号は，決して齟齬のないように述べられながらも決して破綻の無いように説明しなければなりません．それが見た目のイカツサの原因になっているのですが，記号の意味を理解すれば，数式が伝えたいことを読み取れるようになります．

一例を挙げると，以下の三段論法，

　　一．全ての人間は死ぬ．

　　二．ソクラテスは人間である．

　　三．従って，ソクラテスは死ぬ．

は，人間という集合を $S$ として，個々の人間を $a$，ソクラテスを $b$ とし，「死ぬ」という作用を $P$ とすれば，

　　一．$ \forall a \in S \quad P(a) $ 或いは $ \nexists a \in S \quad \lnot P(a) $

　　二．$ b \in S $

　　三．$ \therefore P(b)$

ってな感じです．$ \lnot $ は否定の記号で，「全ての人間は死ぬ」の対偶を取った「死なない人間は存在しない」としたものも「一」に別表記として書いておきました．

話を戻せば，「モノの数」を表す「自然数」とは上で述べた公理①～⑤に基づく「数」なのだ，と説明されます．

以上を踏まえると，「たろうくんとおかし」の問題は数学的な厳密さを用いるならば，以下のように答えなければなりません．

こたえ

　　$ 2 := \mbox{suc}(\mbox{suc}(0)) $：2とは0の次の次の数ですよん

　　$ 3 := \mbox{suc}(\mbox{suc}(\mbox{suc}(0))) $：3は0の次の次の次の数ですよー

　　とすれば，

　　$ 1 + 2 = 1 + \mbox{suc}(\mbox{suc}(0)) $ と書けて，これは0の次の次の数の次の数なので，

　　$ \mbox{suc}(\mbox{suc}(\mbox{suc}(0))) = 3 $ となるのよ．

　　だから3こ

なお，「プリンキピア・マテマティカ」という本では，$ 1+1=2 $ が証明されるまでには700ページもの準備がなされているそうです．

ときに数学や算数を揶揄するようにも延べられることがある「1足す1がなぜ2になるのか分からない」という疑問も，それはそれで妥当な疑問であるとも言えます．

19.3.不完全性定理

結局，数学がやっていることは，「公理」の集まりである「公理系」を前提として記号を用いて推論を行っていく，という作業となります．

このような考え方を「形式主義」と言います．

そのような形式主義としての数学というものは，一貫していて全く矛盾ないものである，ということを自身が証明できる…と考えられていました．

そのことを実際に示そうと提案したのがダフィット・ヒルベルトです．

この人，渋い！！

詳しい人ならヒルベルト空間など聞いたことがあるかと思います．私たちは日常の中で，例えば東京から大阪までの距離だとか，大阪は東京から西の方角だとか，を考える場合には，数学的には実数範囲のヒルベルト空間を認識しています．

ヒルベルトは数学の形式化とその無矛盾性を示すことを目指してヒルベルト・プログラムを提示しました．

しかしながら，クルト・ゲーデルが「不完全性定理」を提示したことで大変なことが分かってしまいました．

要するに，数学について，

・ある前提の下でいろいろ考えてみると，正しいか間違っているか分からない問題に必ず出くわしますよ．（第1不完全性定理）

・ある前提の下でいろいろ考えて分かったことを使ってその前提自身が正しいか間違っているかということは判断できませんよ．（第2不完全性定理）

ということをゲーデルが数学それ自身を使って証明してしまったのです．

これでは数学が自身の無矛盾性を証明できない！…ということになってしまいます．

ヒルベルトさん，大ショックです．．

不完全性定理は数学的な記述で証明が行われた数学に関する定理なのですが，その言わんとするところが哲学的にも通じるところがあるために，例えば「僕は矛盾したことは言っていないから僕は正しい」ということは証明できない，というようなことにも当てはめられるので，（誤用もあれど）結構幅広く引用されることがあります．

ということで，数学が抱える問題が顕になったわけですが，しかしこれは数学の限界を示すものではありません．もしある公理系が無矛盾であると証明したければ，その公理系よりも強い公理系を使って証明すれば良い訳です．

このことはむしろ，数学が弛まぬ発展を続けるべきであるという大きな動機付けになったのではないでしょうか．

19.4.数学の分類

数学をざっくり分類すると，異論あるやもですが，以下のようになります．

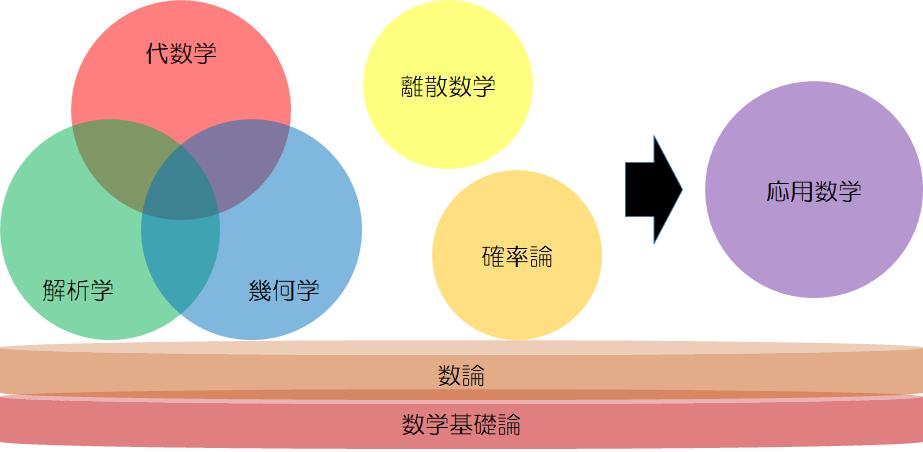
$数学の分類$

数学は数学基礎論や数論を土台としています．

離散数学や確率論は離れて描いていますが，独立しているとも言えません．また応用数学は，応用と言いながら，確かに数値解析や最適化問題のような工学的なものもありますが，カオス理論やフラクタルのような純粋数学の要素も含みます．

なお統計学は数式がたくさん出てきますが，一般には数学には含まないものとなっています．

いずれにしても大きな3本柱は「代数学」「解析学」「幾何学」であることには異論ないかと思われます．

代数学は，数の代わりに文字を用いて方程式の解法を研究する学問に端を発し，次第に抽象代数学へと発展して，今ではある数の集合とその算術によるそれ自体またはその結果の代数的構造を調べるものになっています．

例えば，2つの数 $a$ と $b$ の加法（足し算）である代数系 $(a, b, +)$ はどんな性質を持つか，というようなことです．

解析学は，無限の概念を扱うもので，その基本的な部分は微分や積分となります．

例えば，ある関数 $f(x)$ において，$x$ が無限小だけ変化するときの $f(x)$ の変化はどうなるか，というのは微分の考え方です．

幾何学は，図形や空間の性質について研究するものです．

簡単なところでは，ユークリッド幾何学では平行線は交わらないとか三角形や円についての性質に始まり，ひいてはボールとコップは同じであるが，ボールとドーナツは違っているというようなことを取り扱う位相幾何学も含まれます．

数学の分類については，こちらもぜひご参照ください．

19.5.数学と物理学

さて，ということで，数学を実際にこの宇宙を現象論的に説明しようと試みる「物理学」に適用した場合にはどうでしょうか．

幸いなことに，事象というものは，ある条件を満たせばそれを再現することができます．或いはある条件下で発生する事象を観察することができます．

森の中で人知れず木が倒れた．さて「木が倒れた」という事象は存在するか．

これは人間原理に関わる命題であって，街中で議論している限りは哲学的な命題ですが，これを物理学として取り扱うのであれば，実際に森に行って，木が倒れているかどうかを調べれば良い訳です．

もし木が倒れていればその事象は存在するし，森の中でずっと観察して木が倒れるところを見れば，人間を前提としなくても，それを自然の摂理で説明することができます．

即ち，物理学の方で既知の事象からこれを理論として数学的に表現できた，そしてその理論から未知の事象が演繹的に導出されたとしましょう．

さて，その理論は正しいか否か？

これを検証せねばなりません．

もし一つでもその理論に反することが観察されれば反証となるので，その理論は修正が必要になります．

しかし未だかつて反証が挙げられない場合，むしろその理論から演繹的に予測された事象が複数回観察される場合には，その理論は「正しい」…ではなく「矛盾していない」と解釈するのが「科学」です．

矛盾していないから，今の内はその理論を使っていろいろやっていきましょう…というスタンスです．

相対性理論はそれまでの絶対空間，絶対時間というものが存在しないことを主張しました．

そして水星の近日点移動や，最近では重力波といった，相対性理論が予測した事象が再現性良く観測されました．

今のところ，相対性理論の反証が見付かっていない以上，とりあえずは現状の範囲では矛盾が見付かっていないから，うまく利用して行きましょうということで，私たちも日常的にカーナビやスマホでGPSを用いて位置情報を得ています．GPSは相対性理論に基いて構築，運用されています．

相対性理論の検証は今もなお続けられていますが，現在，物理学者が模索しているのは，相対性理論を包括するより上位の自然法則が恐らく存在するだろうという，この宇宙の現象全てを説明することのできる，万物の理論とも呼ばれる統一理論の完成です．

このように，物理学は現状，数学を有効な手段として大いに利用して，事象と解釈との客観的，普遍的な一対一対応を目指していますが，その対応には事象から理論への帰納と，理論から事象への演繹とが互いにうまく作用し合うことによって検証が行われ続けています．

そしてもし一対一対応が崩れるようなことが見出されれば，事象は（実験や観測に人為的なミスがなければ）神様の所業なので疑う余地はなく，従って解釈に修正が施されます．

カール・セーガン曰く，科学とは自己修正的である．

そのような権威や権力，人間原理に囚われない自己修正を何度も何度も経て，今の科学があって，その科学の成果を用いて自然法則をうまく利用して宇宙のシアワセを追求するのが工学であり，工学は技術を生み出します．

アラタはコクーンでの工学者としての立場に苦悩しているようですが，地球上の工学の住人である筆者はそれを念頭に，心して工学の使命を追求していく所存です．

epi.19 - makeup class

19.数学と物理学をほろほろと