epi.14
14.最適な道を選ぶ
本作ではところどころに数式が登場します.
その数式はその話の中で関連するものや宇宙考証にあたっての検証で使用したものを提案し,作者によって美しく漫画の中で採用されています.
特に今話では,宇宙工学の分野でもなかなかとっつきにくい数式が登場します.
その意味をご理解いただかなくてもストーリーには影響ありませんが,もしご興味あればその数式が熱烈に伝えようとしているコトを感じみ取って頂けると,なお嬉しく存じます.
また,モノヅクリの方が注目されるであろう今話のひとコマについても紹介します.
14.1.徳島へ行こう!
突然ですが,みなさまは徳島に行かれたことがあるでしょうか?
既に行かれた方には,ありがとうございます,何もないところですが良き想い出となっていれば嬉しく思います.
また,これは大変重要な情報ですが,徳島といえば本作の吟鳥子先生がご在住ですし,前作「アンの世界地図」の舞台の一つでもあります.
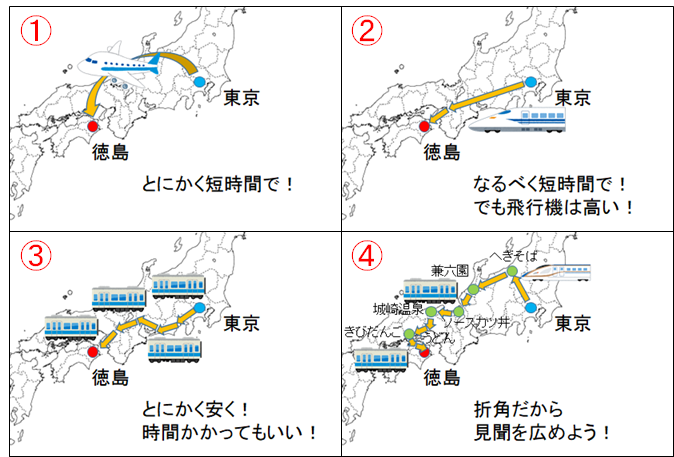
東京から徳島へ行くことを考えてみます.
トップ画像のようにいろいろな経路が考えられます.
①左上は,費用は幾らかかっても良いからとにかく短時間で行く場合です.すると必然的に飛行機で…となり,羽田空港から徳島空港へはJALさんの路線があります.私のような地方出身者にとっては,他の航空会社が状況により羽田~徳島便から撤退したり戻って来たりしていた中で,経営が厳しいときでもずっとずぅーっと路線を維持してくれていたJALさん♥には心から感謝しています♥♥♥
②右上は,なるべく短時間で行きたいけれども,でも飛行機は高いので選びにくい…という場合です.すると東京駅から新幹線でまず大阪や神戸に行き,そこからバスで本四連絡橋を渡る経路となるでしょう.大阪や神戸からのバスはとてもたくさん走っているのでこれはこれで便利なものです.明石海峡大橋や大鳴門橋からの景色はとても美しいですよ!
③左下は,時間はどれだけかかっても良いからとにかく安く行きたい場合です.例えば青春18きっぷなどで,在来線を乗り継ぐものです.東海道本線では静岡の横断がなかなか手強いところですが,カタコトと揺られながら駅弁を食べながら車窓を眺めるのも一興ですね.大阪まで来ればバスですが,一方で名古屋から近鉄と南海電鉄を使って和歌山港へ行って南海フェリーで渡るのも良い感じです.なお東京からは小倉へ行くオーシャン東九フェリーが運行していますが,途中,徳島に停泊します.18時間ほどの船旅ですが,安くて,海からの景色もかなり良い船旅です.
④右下は,折角だから見聞を広めようと,東京から北陸を回っていろんな景色や食べ物を楽しんでみるものです.これだと逆に費用はかかるかも知れませんが,その分,人生の経験値が増えます.遠回りも辞さないということであれば,大阪や神戸からではなく,岡山回りで瀬戸大橋を渡って行くのも良いですね.
以上のように,何を第一とするか,つまり時間を節約するのかお金を節約するのか,或いは両方とも考慮してそこそこのところを選ぶのか,またはそれ以外のことを重視するのかによって,人それぞれ,いろんな経路が選ばれます.
このようなことは旅行に限らず,たまの外食の内容や頻度,パソコンやスマホを買うときの性能と値段…など,いろんな場面でみなさん,折り合いを付けて一つのモノ,コトを選んでいますよね.
何か判断基準となるコトに基いてこれが最大または最小となるように物事を選び,行動を決定することは工学の分野では「最適化問題」とか「最適制御問題」とかと呼ばれています(以降では「最適化問題」と統一して呼びます).最適化問題を解くためのいろいろな考え方や数式が提案されています.
14.2.最適化問題の一例
例えば「100g当たり500円のお肉を買う」というような場合,お肉の量と自分の食欲の程度を照らし合わせてお肉の分量を決めることは,話が単純です.これは「お肉の量」と「自分の食欲の程度」が相反しないからです.この場合は,自分の欲しい分だけを変えばそれでOKです.
ところが,幾つか考えるべきコトがあって,それらが相反する場合には最適化問題として扱う必要が出て来ます.「お肉を買う」ということに対して,「自分の食欲の程度」とは別に「自分の懐事情」を考えなければならないとき,食欲はお肉を増やす方向に働くけれども,懐事情はお肉を減らす方向に働くため,両者は相反します.
他の例を挙げますと,旅行に行くとき,いろいろなモノを詰め込んで荷物を多くすれば「旅行先で困らない」というメリットがある一方,「カバンが重くなって困る」というデメリットがあります.つまり,旅行先で困らないようにしようと思えば荷物は多くすべきである一方,旅行先で身軽に動けるようにしようと思えば荷物は少なくするべきです.
では,お肉をどれだけ買えば家計をそれほど圧迫することなくそこそこ食欲が満たされるのか,或いは,荷物をどれくらいにすれば旅行先でそれほど困らずまたカバンをある程度軽くできるのか…みなさんもこのようなことを日常的にされているかと思われます…これが最適化問題です.食欲を満たすということ,旅行先で困らないということは,言わば選択を行った結果で得られる「価値」と呼ぶこともでき,これをできる範囲で最大化することが目的となります.
宇宙工学においても,宇宙機に燃料をたくさん積み込めば,噴射が長くできるのでより多く加速できますが,重くなるのであまり遠くへ行けなくなるということがあるため,ある宇宙機に対して燃料の適切な搭載量というものが存在するなど,最適化問題は常につきまといます.
14.3.ハミルトン・ヤコビ・ベルマン方程式
数学に長けた方ならコチラをご覧になれば「なるほど!」となるのでしょうが,私も数学は「長けているか?」と問われれば「それほど…」と答えざるを得ない状況ですので,以下に説明を試みますが拙いものであることを最初に申しておきます.
こちらがハミルトン・ヤコビ・ベルマン方程式となります.
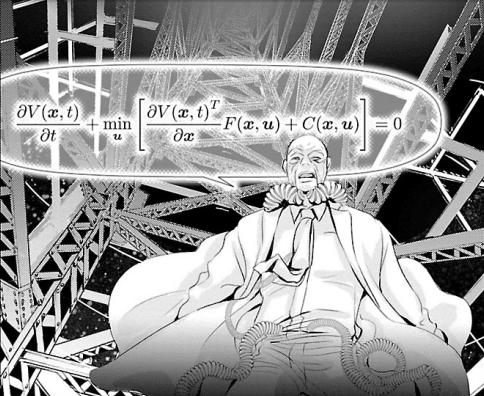
おじいちゃん…くらくらするよ…
くらくらするのは,これが偏微分方程式であるから…微分積分というものは,偏微分が出て来ると一気に難しくなる…と個人的には思います.
くらくらが収まらない!という方は,以下の赤字部分をざーっとスクロールして読み飛ばして,下の方の黒字に戻る部分から再度読んでいただければと思います.
まず偏微分について説明します.数学的には,複数の変数で定義される関数の,ただ一つの変数の変化に対する変化の割合…ということなのですが,難しいですよね..
コーヒーを甘くしようとすれば砂糖を入れます.そして「砂糖の分量」に対して「コーヒーの甘さ」は直接かつ一意に調節することができます.つまり,砂糖の分量でコーヒーの甘さが決まるということなので,「コーヒーの甘さ」は,正比例とは言えないかも知れませんが(人間の感覚器は対数的とも言われます),「砂糖の分量」の関数になっています.
それに対して煮物です.煮物を美味しく味付けするときには砂糖,塩,みりん,だし,醤油などを入れますよね.だから「煮物の美味しさ」は,「砂糖の分量」と「塩の分量」と「みりんの分量」と「だしの分量」と「醤油の分量」,そして「煮る時間」…の関数になっています.
ここで偏微分とは,調味料ひとつ,例えば砂糖を少し加えると煮物の美味しさがどれだけ変化するか,ということを求める演算となります.
ところが砂糖を加えて変化する煮物の美味しさの変化の割合って,他の調味料の入れ具合とか煮る時間によっても変わりますよね.
つまり,「砂糖の分量」によって変化する「煮物の美味しさ」は,今時点での全部の調味料の入れ具合の「状態」と砂糖を入れるタイミング,言うなれば「時刻」によって変わってきます.
いま宇宙機が太陽や惑星の重力に従って軌道運動をしながら,ある惑星へ向かいたいと思っているとします.
重力のなすがままに運動するのが一番楽です.何もしなくても軌道運動によって無動力で航行するからです.しかし目的の惑星へ行けるとは限りません.目的の惑星へ行くためには,推進機によって噴射を行い,その推力によって軌道を調節しなければなりません.噴射を行うということは,それなりの推進剤を消費します.しかもその推進剤の消費によって得られる軌道の変化量というものは,「いつ」「どこで(=状態の一種)」噴射するかによって変わって来ます.
つまり,「軌道の変化量」は,噴射をする時点での宇宙機の「状態」と噴射をする「時刻」によって変わってくるものなのです.
そこで,位置などの宇宙機の「状態」を表すパラメータを \( x\) ,噴射のタイミング即ち「時刻」を \( t\) と表し,これによって決まる軌道の変化量などの何らかの「価値」を \( x\) と \( t\) の関数として \( V(x,t)\) と書くこととします.ここでの価値は「軌道の変化量」とは限らず,徳島へ行くときと同じく,所要時間だったり燃料の消費量だったりなどいろいろ設定することができ,それによって答えも変わって来ることにご注意ください.
その「価値」が,いつ噴射するか?どれだけ噴射するか?という時刻や時間のみが変化したときにどれだけ変化するかを表したものが偏微分 \( \frac{\partial V(x,t)}{\partial t}\) であり,ハミルトン・ヤコビ・ベルマン方程式の第1項に現れています.
あぁ帰らないで…ガンバりましょう!
また例え話から始めます.
いま北に向かって登りになっている斜面があるとし,高いところに行くほど褒められるという「価値」が得られるものとします.
この斜面を歩くとき,北に向かえば勾配は最大なのでとてもしんどいですが高いところへ行けます.南に向かえば下り坂なのでとても楽ですが褒められません.また,東や西に歩けば勾配はゼロなので平坦な道を歩いているのと同じであって,特に褒められ方に違いは生じません.
さて,先述のように「価値」は「時刻」だけでなく「状態」でも変化することは述べました.一般的には,ある時刻において自分は「高度」=「価値」という凸凹のある広がりの中の,ある位置,即ち状態に佇んでいることになります.「価値」を高めるにはより急勾配な登りの向きに進めば良いことになります.その状態での「勾配」を表すのが偏微分 \( \frac{\partial V(x,t)}{\partial x}\) です.この例では北向きに最大の勾配があることが計算により求まります.
次に,どの方向に進むかということを考えます.
東西南北によってしんどさが変化するのがお分かりかと思います.
北向きが一番しんどい,東西は平坦と同じなので歩くしんどさ程度,ところが南向きだと下りなのでホイホイと楽に進むことができます.
「歩く」という自分の身体の「操作」によって動くことは,どの「位置」にいて,どのくらいの「操作」を行うかということでその程度が変わってきます.
同じように宇宙機もまた,どの「位置」にいて,どのくらいの噴射という「操作」を行うかによって軌道の変化量が違ってきます.既に「位置」は \( x\) で表すこととしていますので,ここでは新たに「操作」を表すパラメータを \( u\) と書くことにします.これによって宇宙機の動きは \( F(x,u)\) という関数で表せるものとします.
「価値」という山の最も急勾配な向きに動くことが最も効率良く「価値」を高めることができますが,最もしんどいです.つまり,宇宙機の進む向きによって「価値」の高まり具合が異なり,それに対応するしんどさもまた異なって来ます.この「宇宙機の進む向きによるしんどさ」を求めるものが,ハミルトン・ヤコビ・ベルマン方程式の第2項のカッコの中の一つ目の \( {\frac{\partial V(x,t)}{\partial x}}^T F(x,u)\) です.先述の「勾配」に対する「宇宙機の進む向き」が重要なのでこのような演算では内積が便利なのですが,それぞれがベクトル量なので転置記号で内積であることを示しています.
宇宙機の動きをもたらすためには推進剤を噴射(つまり消費)するというような何らかの「コスト」を要しますが,そのコストはどの「位置」でどのくらい噴射という「操作」を行うかで異なって来るので,これをハミルトン・ヤコビ・ベルマン方程式の第2項のカッコの中の二つ目では \( C(x,u)\) という関数で表現します.
以上より,ハミルトン・ヤコビ・ベルマン方程式の第2項は,価値を高めるためにどのくらいしんどくてどのくらいコストがかかるか,という「負担」の程度を表しているとも見ることができ,これが最小となるようにするということを表現しています.
そして,そもそもは何も無いところから自分の「負担」によって「価値」というものが初めて生まれ,自分の「負担」に応じて増減するものです.従って,時々刻々の「価値の増減」と「負担の大小」の合計は釣り合ってゼロとなる必要があります.
この計算によって,「負担」を最小としつつ,その中で「価値」をできるだけ最大にするような宇宙機の「負担」の時間履歴が求まります.そして負担の中の「操作」の計算結果に応じて,実際に宇宙機を噴射して軌道を制御することになります.ある惑星へ向かう宇宙機については,負担を最小とするということは燃料の消費量や所要時間を最小とすることであり,価値を最大にするということは目的の惑星へ到達するということに相当します.
これが,おじいちゃんがアラタに伝えた数式です.
ここから黒字に戻りますね.
分かりやすい例を挙げれば,以下の通りです.
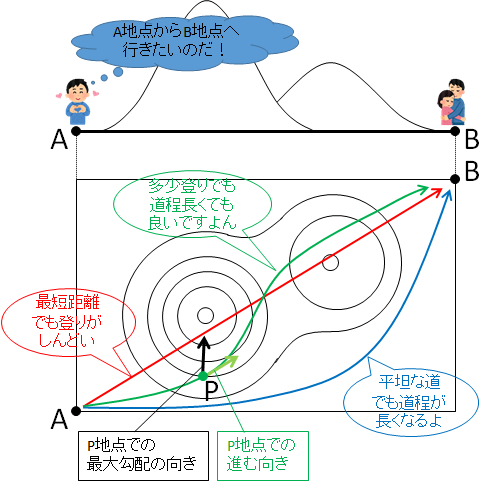
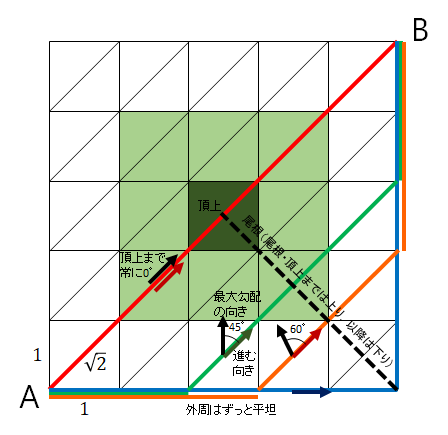
ある人がA地点からB地点へ行きたいと考えていますが,その途中には山が幾つかあります.
P地点における最大勾配の向きと実際に進む向きも図示しました.
歩く距離(道程)を最小化することを価値と定義してやれば,最短の赤の経路が求まります.しかし高い山を乗り越えねばならないので,とてもしんどいです.
一方,しんどさを最小化することを価値と定義してやれば,比較的平坦な青の経路が求まります.登りが殆どないので楽なのですが,道程が長くなって所要時間が増えます.
だから,ある程度はしんどくても良いからある程度は所要時間を少なくするようなところを歩きたい…それをハミルトン・ヤコビ・ベルマン方程式を使って計算すれば,緑の経路のようなある道筋とともに,その道筋を進むためにどのような「操作」をすれば良いかが求まります.どのくらいしんどさや所要時間を許容できるかということを予め設定しておくと,緑の経路は幾らか変化します.
これをもっと単純にして下図のような5×5の格子を考え,左下をA地点,右上をB地点とし,A地点とB地点の間には山が一つだけあるとします.
いまA地点からB地点へ向かうのですが,経路としては右向き,上向き,右斜め上向きだけが進むことが許されているとします.
するとA地点からB地点までの経路は幾つかありますが,その中で4つだけ考えてみます.即ち,最短距離の「赤の経路」,最も楽そうな「青の経路」,その間の「緑の経路」と「橙の経路」です.
進むときには,平坦だろうが傾斜があろうが,道程1当たり体力は1だけ必要だとします.
上りの場合は「身体を持ち上げる」という「操作」が必要となります.ここではこちらやこちらなどを参考にして,上りの場合は平坦な道を歩く場合と比べて3倍の体力を要するものだとして,最大勾配の向きと進む向きの間の角度に応じて別途体力を必要とするものとします(詳細は下図ご参照).
一方,平坦な道や下りの場合は歩くこと自体には変わりなく,また下りでは一見楽そうではありますが身体にかかる外力に抗うことなく進むという点では平坦な道と変わりがないと仮定します.
以上に基いて4つの経路について道程と必要体力(コスト)を求めると,以下のようになります.
つまり,道程の短い順では赤→緑→橙→青の順となっている一方,コストで見れば楽な順では青→橙→緑→赤の順となっていることが定量的に求められます.

ではこの中でどの経路をどういう基準で選ぶか,ということを決定しなければなりません.
トップ画像の東京→徳島の例と併せて考えてみます.
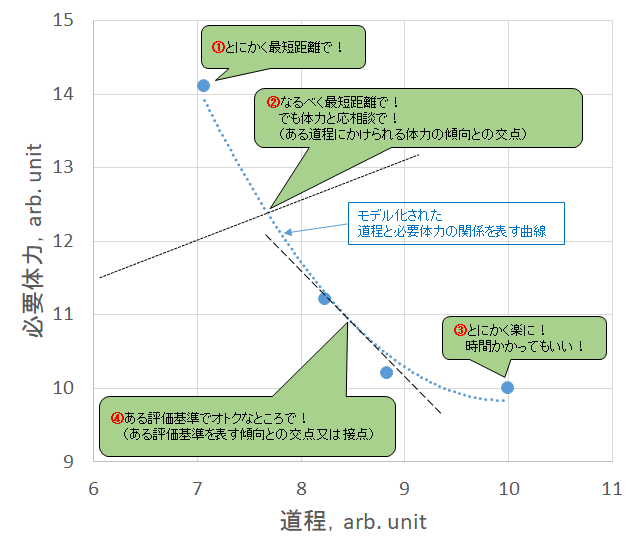
なお下図では,上記で求めた各経路の道程と必要体力をプロットしたものが青の●印,これに近似曲線を当て嵌めて補間することでモデル化したものが青の点線で示されています.上図の中を歩く限りは,この青の点線で示される関係からは逃れられないということを意味します.
①の場合は「とにかく最短距離で!」となって,上図での赤の経路を選ぶことに相当します.体力は最も要しますが,道程は最短ですので最も早く到着することが出来ます.
②の場合は「なるべく最短距離で!」と要求しつつ「自分の体力の範囲内で!」という制約があります.つまり,ある道程に対して自分がかけられる体力の上限が決まっているとすると,下図のようにそれはある関数(下図では黒の点線)で表されます.従って,青の点線と黒の点線の交点が,自分の体力の範囲内で最適な経路であると判断され,上図での緑や橙のような,途中で多少の上りを経験しつつショートカットする経路が選ばれます.
③の場合は「とにかく楽に!」に相当します.従って,必要体力が最小となる,平坦な道だけの青の経路が上図の中で選ばれます.
④の場合は,何らかの別の評価基準,例えば足を動かす回数とか上りでの高度変化とかの上限があるなどして,そこから道程と必要体力との間に何らかの関係が導かれるような場合です.下図ではその関係を,一例として黒い破線で示しています.つまり,選ぶべき経路はこの黒の破線で示される関係を満たしていなければならないということなので,黒の破線と青の点線の交点又は接点が最適な経路であると判断され,②の場合と同じく緑や橙のような経路が選ばれます.ただ②と異なるのは,道程や必要体力とは別の何らかの評価基準も考慮して選ばれる経路であるという点です.
そうして求まった経路について,その経路を辿るためにどのような「操作」を行えば良いかということが求まります.
以上のようなことが,ハミルトン・ヤコビ・ベルマン方程式において表現されています.数式はある物事の考え方を定量的かつ客観的に表現するためのものなので,その意味を紐解けばその考え方を文章で記述することができます.
端的にいえば,祇園さんは「あなたができる範囲で最適な道を見付けなさい」と伝えたかったのではないでしょうか.
どうもおつかれさまでした…
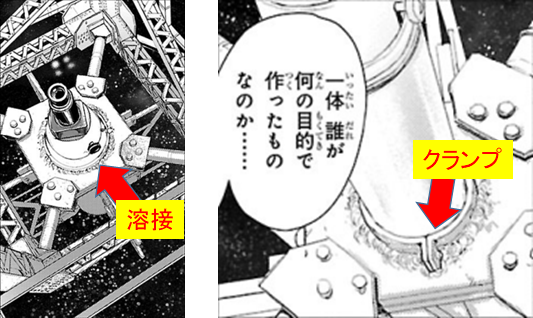
14.2.溶接の機能美
宇宙工学に限らず,構造物を組み上げるときは部材同士を合わせて固定する必要があります.
この固定にはいろいろな方法があって,よくあるのは「ボルト留め」と「溶接」或いは「ろう付け」です.
ボルト留めは,部材に穴やネジ穴を開けておいてネジやボルトで挟み込んで留めるものですので説明は不要かと思われます.
それに対して溶接とは,アーク放電やガス燃焼によって局所的に高温にして部材の一部を溶かし,相手方と一体にして固定するものです.なおろう付けは部材自身ではなく「ろう材」を溶かして部材を固定するものなので接着剤と同じようなものとなので「溶接」とはまた異なるものです.
今話の中では「覗き窓」が東京タワーのてっぺんに溶接で固定されていますが,とても美しい溶接模様が描かれています.
工学の分野で何かを実現しようとすれば,ちゃんとできているものは望むべき機能を発揮しながら大変美しいものとなります.これは「機能美」とも言えます.
慣れない人が溶接をすると,溶接の痕は汚いものとなって,必要な強度を保証できません.しかし熟練した職人が溶接をしたときは適正な強度を実現しつつ,見た目にもそれはもう大変美しいものです!
「美しい溶接」とググッてみました.いやぁ見ていて飽きません!「汚い溶接」のものとは大違いです.私は学生時代の工作実習でしか溶接を経験したことがありませんが,それはもう汚い汚いものでした..熟練した職人さんの技には惚れ惚れさせられます!
作者がきちんと美しい溶接を描かれていることに感服した次第です.
なお,長くて重い棒や円筒の部材を平板に固定しようとするとき,直接溶接をすることは強度的に問題が出てくる場合が多いです.
このようなときにはまず平板に短い円筒部材を溶接しておき,この短い円筒部材に長い円筒部材を突き合わせ,クランプで挟み込んで固定することもよく行われます.このクランプ,そして挟み込んだクランプをボルトで締め付けていることもきちんと描かれています.