1.1.万有引力

万有引力とは，質量を持った物体同士が互いに相手を引き寄せる力です．

私たちは地球の表面にいて，地球と私たちは互いに万有引力によって引き合っています．しかし地球の方が遥かに質量が大きいので，私たちの方が地球に引っ張られていると感じていて，単位質量当たりのその力の大きさは1G（$=9.80665\mbox{[m/s$^2$]}$）と定義されています．万有引力の大きさは天体の質量や天体からの距離によって異なります。例えば月面上では0.165Gであって，地球で体重60kgの人ならそれを支える筋力があるので月面上では体重が60kg×0.165G＝9.9kgになったかのように感じます．火星表面だと0.38G，木星表面（だと定義される場所）だと2.5G，太陽表面（だと定義される場所）だと28G…という具合です．さらに，物体の運動の加速の大きさを表す場合にもG単位が用いられることがあり，アポロ宇宙船が打ち上げられるときに宇宙飛行士が感じる加速度は6Gだとか，スペースシャトルだと最大3Gだとか，旅客機の離陸時の滑走路上での加速度は0.2G程度だとか…と使われます．

距離 $r$ だけ離れた質量 $m$ 及び $M$ の二つの物体の間に働く万有引力の大きさ $F_G$ は，万有引力定数 $G=6.67408 \times 10^{-11}\mbox{[m$^3$kg$^{-1}$s$^{-2}$]}$ を用いて，

$$F_G = \frac{GmM}{r^2}$$

と表されます．ここで，例えば人工衛星（質量 $m$）と地球（質量 $M$）のように，$M$ が $m$ よりずっと大きい（$M \gg m$）とみなせる場合には，地球は動かないと仮定して差し支えありません．$F_G$ を人工衛星の質量 $m$ で割ると，地球が人工衛星に及ぼす加速度 $a_G$ が求まります．これらには，万有引力（Gravity）による力や加速度ということで，添字 $G$ を付けておきます．これを地上での重力加速度 $g=9.80665\mbox{[m/s$^2$]}$ で割ると，我々が日常感じている地球の重力の何倍が働いているかという指標としての加速度（単位G）で表すことができます．

$$a_G = \frac{F_G}{m} \mbox{[m/s$^2$]} = \frac{F_G}{mg} \mbox{[G]}$$

万有引力は常に中心天体（例えば地球）の方を向き続けるので，向心力となります．ある一定の速度を持っている物体（例えば人工衛星）に向心力が作用していると，その物体は次節のように中心天体の周りを円運動します．

1.2.遠心力

遠心力とは，回転運動をしている物体や人が感じる慣性力の一つです．

慣性力とは，加速度を受けている（即ち非慣性系にいる）物体や人が，実際には存在していないのに，まるで存在しているかのように感じる「見かけの力」のことです．

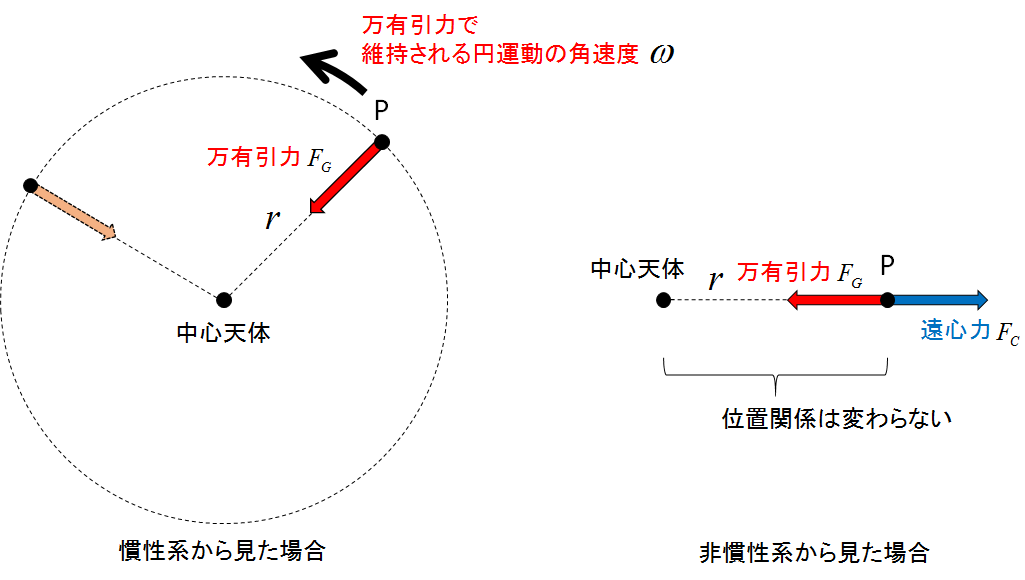
上図左のように，物体が点Pにあって，万有引力によって中心天体の周りを円運動しているときには，その中心天体に向かう方向に常に向心力が働いています．点Pの位置は円運動によって時々刻々と変わるので，向心力の向きも常に変化しています．つまり円運動をしている物体は常に加速度運動をしていることになり，従ってこの物体は非慣性系にあります．

この運動は，これを見ている人の立場によって異なって表現されます．

物体の円運動を傍らで静止している人から見ると，これは慣性系から見ていることとなり，上図左のように物体は万有引力による向心力によって円運動をさせられていると解釈されます．ここに遠心力なんて考える必要性はありませんし，むしろこの人は遠心力が存在しているなんて考えもしません．

一方，物体に乗っている人から見ると，この人は非慣性系から見ることとなり，上図右のように，中心天体は常に同じところにあるように見えます．メリーゴーランドに乗って中心の柱だけを見ていると，メリーゴーランドが回転していてもその柱はずっと同じところにあるように見え，自分との位置関係や方向が変わらないのと同じです．ところで万有引力はこの人も存在していることを知っていて，実際に影響を受けています．しかし万有引力だけが働いているとするならば，この物体は中心天体にまっすぐ落ちていくだけであって，中心天体が常に同じところにあるように見える現実との相違があります．従って，中心天体がずっと同じところに見え続けるためには，万有引力と釣り合う何らかの力が存在していると考えなければ物理的に成り立ちません．これが遠心力です．そして，この人は遠心力を実際に感じることができて，確かに存在することに疑いの余地はありません．

このように，実際に存在している力（慣性系と非慣性系の両方で感じる力）とは異なり，非慣性系でのみ感じる力のことを慣性力といいます．遠心力は慣性力の一つです．

遠心力 $F_C$ は，円運動の半径 $r$ とその角速度 $\omega$ を用いて，

$$F_C = r{\omega}^2$$

と表されます．ここで $\omega$ はラジアン単位での角速度（rad/s）で表すとそのまま上式に代入できますが，度単位での角速度（deg/s）の場合には，度をラジアンに変換する（180°で割って円周率 $\pi$ を掛ける）必要があることに注意してください．これを円運動をしている物体の質量 $m$ で割ると遠心力による加速度 $a_C$ が求まり，さらにこれを地上での重力加速度 $g$ で割ると，G単位で表すことができます．遠心力（Centrifugal Force）による加速度ということで，添字 $C$ を付けています．

$$a_C = \frac{F_C}{m} \mbox{[m/s$^2$]} = \frac{F_C}{mg} \mbox{[G]}$$

上図左のように中心天体からの距離 $r$ の円軌道を周回している物体については，以下の関係式が成り立ちます．

$$F_C = F_G$$

1.3.テザーによる引張力

上記の円運動をする物体が中心天体とテザーで接続されている場合であって，遠心力が万有引力よりも大きい場合には、その差分の力はテザーを引っ張ります．

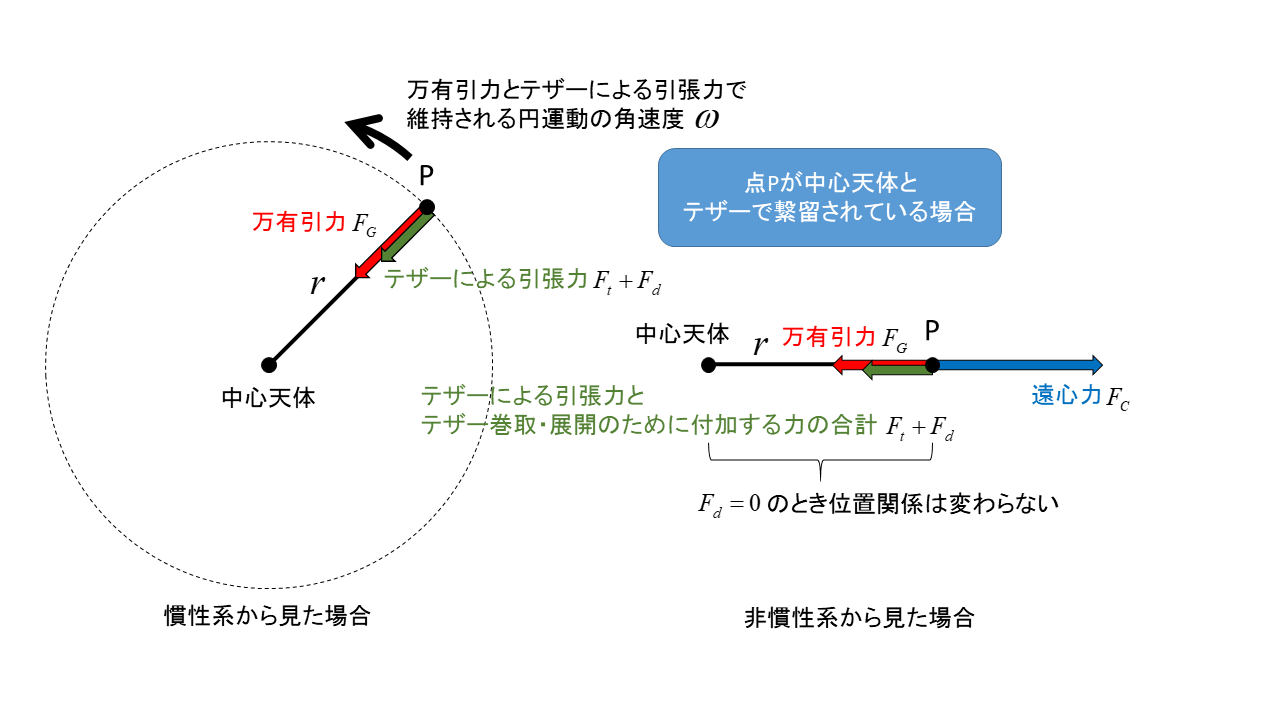
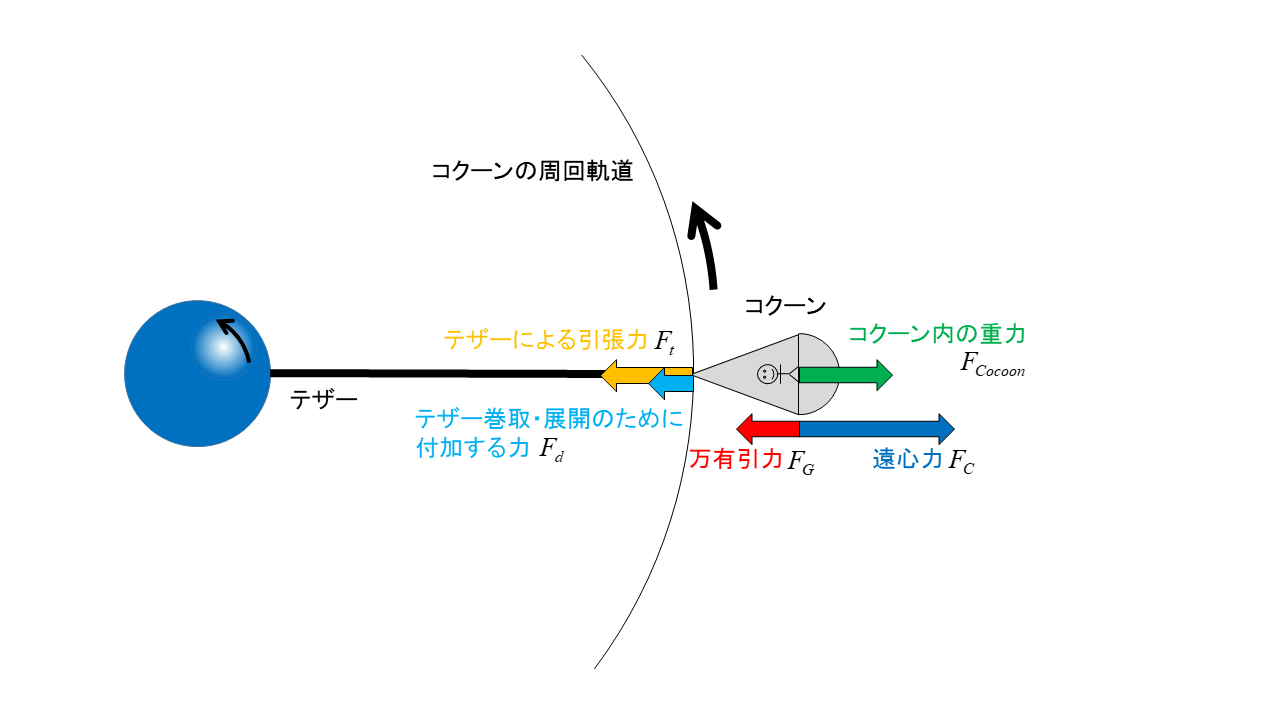
下図で，万有引力よりも遠心力の方が大きい場合（$F_G<F_C$），もしテザーがなければ，この物体は外側へ放り出されます．しかし物体は相変わらず円運動を続けることから，万有引力と遠心力の差分 $F_C-F_G$ はテザーに負荷されることになります．これをテザー張力と呼びます．コクーンにしてみれば，テザー張力の反作用によって遠心力と万有引力の差分がテザーによる引張力として作用するので，テザーによる引張力が向心力として働いています．従って，このテザーによる引張力 $F_t$ には以下の関係が成り立っています

$$F_C - F_G = F_t$$

さらに，この物体がテザーを巻き取る場合，例えばコクーンが地球降下するときにはテザーを手繰り寄せて高度を下げます．このテザー巻取・展開のために付加する力を $F_d$ とし，これはテザー張力による向心力に上乗せされるので，

$$F_C - F_G \neq F_t + F_d$$

という関係にあって，釣り合いが崩れるのでコクーンは半径方向に移動します．

もし $F_d=0$ ならばコクーンは円運動を続けますが，$F_d > 0$ のときはコクーンが高度を下げ，つまり「地球降下」します．

1.4.コクーン内の重力

先述の通り，コクーンが「地球降下」していないときのコクーン内の重力は遠心力と万有引力の差分ですが，「地球降下」をする場合も含めて一般的に記述すると，コクーン内の重力 $F_{Cocoon}$ 及びそれによる加速度 $a_{Cocoon}$ は以下のように求まります．ここで，$a_t=F_t/g$，$a_d=F_d/g$ であり，向きは地球に対して外向きが正の値となります．

$$F_{Cocoon} = F_C - F_G + F_d = F_t + F_d$$

$$a_{Cocoon} = a_C - a_G + a_d = a_t + a_d$$

コクーンがアポジにあるときについて考えると，$a_C$=1.28G，$a_G$=0.28G と求められ，さらに「地球降下」していないので $a_d$=0G であり，コクーン住民にとっては外向きに $a_{Cocoon}$=1.28-0.28=1G の重力が働くように感じられ，下図のような向きで生活することができます．

1.5.コリオリ力

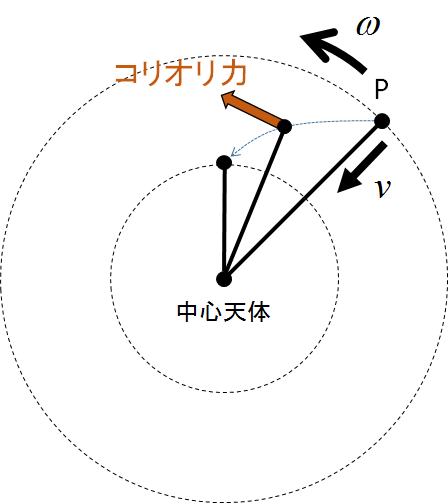
コリオリ力とは，下図のように回転運動をしている物体が回転中心へ向かったり遠ざかったりするときに，回転方向へ働く慣性力です．

簡単な思考実験をしてみます．

あなたはいま立ち止まって，その場で右回りにぐるぐると回転しています（非慣性系にいることになります）．周りの景色はあなたの周りを左回りにぐるぐる回っているように見えます．そのとき，あなたはボールを自分自身に対して前へ放り投げたとします．するとボールは，あなたから見て左側へ飛んでいくように見えます．非慣性系にいるあなたから見れば，あたかもボールに左向きに力が働いたから左側へ飛んでいったとしか思えません．この力がコリオリ力です．しかし傍らで立ち止まって見ている人の立場（慣性系にいることになります）から見ると，ボールは投げられた方向以外への運動の変化は認識されず，つまりコリオリ力なんて存在しないように見えます．

他の事例では，台風の渦巻きが挙げられます．北半球では，赤道の近くで発生した台風は北上します．このとき，台風は，北上することで地球の自転による回転半径（自転軸までの距離）が小さくなるので，コリオリ力によって東向きにそれる向きに力を受けます．ところで大気は地球とほぼ一体となって自転しているので，台風から見れば相対的に，台風の北側の大気は西向き（向かい風）に，南側の大気は東向き（追い風）に動いているように見え，その結果，台風の目を中心に左回りに渦が発生します．

また，砲術では，砲弾の弾道へのコリオリ力の影響は特に南北方向の場合には顕著であって，ゴルゴ13ことデューク・東郷もまた，長距離射撃においてコリオリ力を考慮した狙撃を行っています．

さらに細かいことを言えば，野球でピッチャーとキャッチャーが南北方向にいる場合には，例えストレートを投げたとしても0.何mmかはコリオリ力の影響で球筋がずれます．

コリオリ力 $F_{cor}$ は，角速度 $\omega$ で回転運動している質量 $m$ の物体が，回転中心への方向に速度（動径方向速度） $v$ で動くとき，下式のように求められます．

$$F_{cor} = 2m \omega v$$

これを，回転運動をしている物体の質量 $m$ で割ると，コリオリ力による加速度 $a_{cor}$ が求まり，これを地上での重力加速度 $g$ で割るとG単位となります．コリオリ力（Coriolis Force）による加速度ということで，添字 $cor$ を付けています．

$$a_{cor} = \frac{F_{cor}}{m} \mbox{[m/s$^2$]} = \frac{F_{cor}}{mg} \mbox{[G]}$$

コリオリ力の作用する向きは，動径方向速度 $v$ が回転中心へ向かう向きの場合には回転の向き（前向き）に，逆に回転中心から離れる向きの場合には回転の向きの逆（後向き）になります．これはベクトルで表記すると一目瞭然なのですが，ここでは割愛させていただきます．このことは，紐に錘を付けて，紐の一端を手で持ってぶんぶん振り回しているときに，紐を短くしていくと錘が前に寄っていき，逆に長くすると後ろに寄っていくことを見ることができるので，身近に実験することができます．

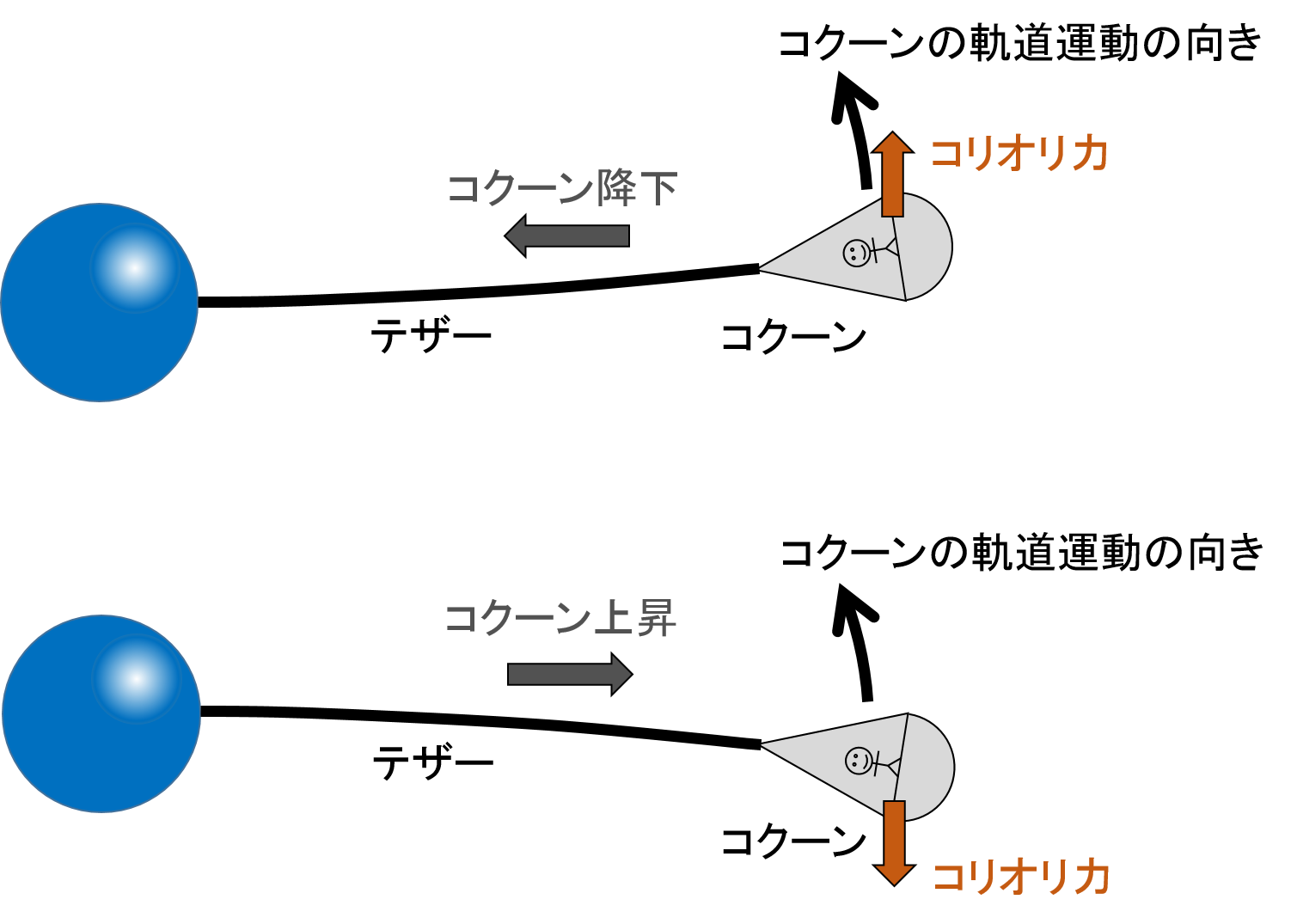
コクーンの場合，下図のような向きにコリオリ力が作用して，テザーが湾曲します．このときコクーン住民は，重力の方向に対してほぼ垂直な方向にコリオリ力を感じるため，両者が合わさることで，ぐわんと目が回るでしょうし，頭を動かしたり歩いたりするとふら～っとするような感覚を覚えることでしょう．これによって，目では動いていないように見えるのに三半規管はコリオリ力を感じてしまうので，平衡感覚に支障が生じ，人によっては気持ち悪くなるコリオリ酔いが発生します．メリーゴーランドで余りきょろきょろと顔を動かしていると気持ちが悪くなるのと同じです．

また，第2話の扉絵でも，コリオリ力によってテザーが湾曲していることが描かれています．

1.6.オイラー力

オイラー力とは，回転運動の角速度が変化する（角加速度が加わる）ときに回転方向に感じる慣性力です．

これも思考実験が簡単です．

メリーゴーランドに乗っているとき，メリーゴーランドが動き始めると身体ががくんと後向きに引かれるような力を感じます．これがオイラー力です．回転運動ではなく直線運動でも加速時に座席に押し付けられるような後向きの力を感じますが，これと同じことです．メリーゴーランドに乗っている人（非慣性系にいる）には突然後向きの力が作用したようにしか思えないのですが，傍らで見ている人（慣性系にいる）にとっては単にメリーゴーランドが回り始めたので，作用反作用の法則でいうところの反作用が作用しただけのことにしか見えません．

同作では，コクーンの軌道運動について，回転方向には積極的な加減速を行わないのですが，後に解説するコクーンの運動を数式で記述するときには一つの項として出てきます．

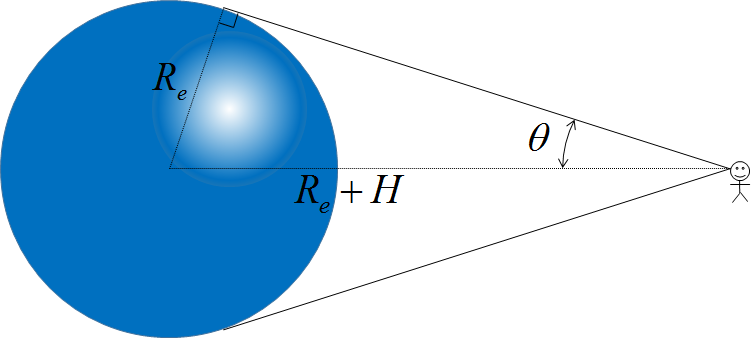
1.7.地球の見え方

地球の視角は，下図を用いれば $2\theta$ となります．地球半径を $R_e$，コクーン高度を $H$ とすると，幾何学的な関係から，

$$\theta = \arcsin \frac{R_e}{R_e+H}$$

が成り立ちます．また満月を基準にする場合，満月の視角は約0.5°なので，$2\theta$ を0.5°で割れば求まります．

epi.1 - makeup class

1.コクーンに働く力